|
Unterrichtseinheit
Ganze Zahlen
|
Ganze Zahlen Definitionen Die Menge 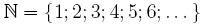 heißt Menge der natürlichen Zahlen. heißt Menge der natürlichen Zahlen. Die Menge 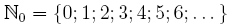 heißt Menge der natürlichen Zahlen einschließlich der Null. heißt Menge der natürlichen Zahlen einschließlich der Null. Die Menge 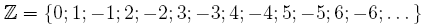
heißt Menge der ganzen Zahlen. Die Begriffe negativ und positiv: 
Von zwei ganzen Zahlen a,b heißt -
a kleiner als b, geschrieben a < b, wenn a auf der Zahlengeraden links von b liegt. Beispiele: – 6 < –5 oder –5 < 4 oder 8 < 9 -
a größer als b, geschrieben a > b, wenn a auf der Zahlengeraden rechts von b liegt. Beispiele: 5 > 4 oder 2 > –3 oder –1 > –2 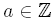 heißt positiv, wenn a > 0 gilt und negativ, wenn a < 0 gilt. heißt positiv, wenn a > 0 gilt und negativ, wenn a < 0 gilt.
Auf der Zahlengeraden liegen die positiven Zahlen rechts von der Null und die negativen links von der Null. |  Merke Merke
Für alle 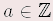 gilt: gilt: | 0 – a | = | – a | | –(–a) | = | a | | (– 1) · a | = | – a | Insbesondere: – 0 = + 0 = 0 und –(–1) = 1 und (–1) · (–1) = 1. |
Beispiele | a) | 0 – 2 | = | –2 | b) | 0 – (–2) | = | 2 | | c) | –(–2) | = | 2 | d) | –(+2) | = | – 2 | | e) | (– 1) · 2 | = | – 2 | f) | (–1) · (–2) | = | 2 | |  Merke Merke
Für alle 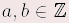 gilt: gilt: | a + (– b) | = | a – b | | a – (+b) | = | a – b | | a – (–b) | = | a + b | | Beispiele | a) | 5 + (–7) | = 5 – 7 | = –2 | b) | 5 – (+7) | = 5 – 7 | = –2 | | c) | 5 – (–7) | = 5 + 7 | = 12 | d) | –5 + (–7) | = –5 – 7 | = -12 | | e) | –5 – (+7) | = – 5 – 7 | = –12 | f) | –5 – (–7) | = –5 + 7 | = 2 |
| Merke Für alle 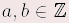 gilt: gilt: | – (a + b) | = | – a – b | | – (a – b) | = | – a + b | | – (–a + b) | = | a – b | | – (–a – b) | = | a + b | | Beispiele | a) | – (2 + 3) | = | –2 – 3 | | b) | –(–2 + 3) | = | 2 – 3 | |  Merke Merke
Für alle 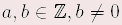 gilt: gilt: | (–a) · b | = | –(a · b) | (–a) : b | = | –(a : b) | | a · (–b) | = | –(a · b) | a : (–b) | = | –(a : b) | | (–a) · (–b) | = | a · b | (–a) : (–b) | = | a : b | | |  Merke Merke
Das Multiplizieren und Dividieren ganzer Zahlen folgt einer einfachen Regel: | ( + ) · ( + ) | = | ( + ) | ( + ) : ( + ) | = | ( + ) | | ( – ) · ( – ) | = | ( + ) | ( – ) : ( – ) | = | ( + ) | | ( + ) · ( – ) | = | ( – ) | ( + ) : ( – ) | = | ( – ) | | ( – ) · ( + ) | = | ( – ) | ( – ) : ( + ) | = | ( – ) | | Beispiele | a) | (+8) · (+4) | = | 32 | b) | (+8) : (+4) | = | 2 | | c) | (–8) · (–4) | = | 32 | d) | (–8) : (–4) | = | 2 | | e) | (+8) · (–4) | = | –32 | f) | (+8) : (–4) | = | –2 | | g) | (–8) · (+4) | = | –32 | h) | (–8) : (+4) | = | –2 | |  Merke Merke
Für alle 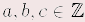 gilt: gilt: | a + b | = | b + a | Kommutativgesetz der Addition | | a · b | = | b · a | Kommutativgesetz der Multiplikation | | (a + b) + c | = | a + (b + c) | Assoziativgesetz der Addition | | (a · b) · c | = | a · (b · c) | Assoziativgesetz der Multiplikation | | a · (b + c) | = | a · b + a · c | Distributivgesetz | | |