|
Unterrichtseinheit
Rationale Zahlen
|
Rationale Zahlen 1. Definition Die Menge 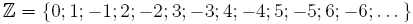 heißt Menge der ganzen Zahlen. heißt Menge der ganzen Zahlen. Die Menge 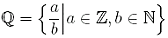 heißt Menge der rationalen Zahlen. heißt Menge der rationalen Zahlen. 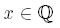 heißt positiv, wenn x > 0 gilt und heißt positiv, wenn x > 0 gilt und
negativ, wenn x < 0 gilt.

Auf der Zahlengeraden liegen die positiven Zahlen rechts von der Null und die negativen Zahlen links von der Null. Von zwei rationalen Zahlen x, y heißt -
x größer als y, wenn x - y > 0 gilt
x liegt dann auf der Zahlengeraden rechts von y. -
x kleiner als y, wenn x - y < 0 gilt.
x liegt dann auf der Zahlengeraden links von y. |  Merke Merke
Für alle 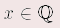 gilt: gilt: | 0 – x | = | –x | | –(–x) | = | x | | (–1) • x | = | –x |
Insbesondere: -0 = +0 = 0 und 1 und (-1) • (-1) = 1.
Für alle x, y 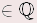 gilt: gilt: | x + (–y) | = | x – y | | x – (+y) | = | x – y | | x – (–y) | = | x + y | |
3. Beispiele | a) | 5 + (–7) | = | 5 – 7 | = | –2 | b) | 5 – (+7) | = | 5 – 7 | = | –2 | | c) | 5 – (–7) | = | 5 + 7 | = | 12 | d) | –5 + (–7) | = | –5 – 7 | = | –12 | | e) | –5 – (+7) | = | –5 – 7 | = | –12 | f) | –5 – (–7) | = | –5 + 7 | = | 2 |

|  Merke Merke
Für alle x, y 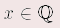 , y , y 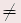 0 gilt: 0 gilt: | (-x) • y | = | – (x • y) | (–x) : y | = | – (x : y) | | x • (–y) | = | – (x • y) | x : (–y) | = | – (x : y) | | (-x) • (–y) | = | x • y | (-x) : (–y) | = | x : y | Für alle 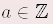 und alle und alle 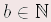 gilt gilt | Insbesondere: | 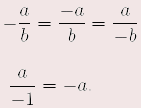 | | |  Merke Merke
Das Multiplizieren und Dividieren ganzer Zahlen folgt einer einfachen Regel: | ( + ) · ( + ) | = | ( + ) | ( + ) : ( + ) | = | ( + ) | | ( – ) · ( – ) | = | ( + ) | ( – ) : ( – ) | = | ( + ) | | ( + ) · ( – ) | = | ( – ) | ( + ) : ( – ) | = | ( – ) | | ( – ) · ( + ) | = | ( – ) | ( – ) : ( + ) | = | ( – ) | | Beispiele (-3 - 7) • (-4 - (-6)) : (-2 - 3) = (-10) • (-4 + 6) : (-5)
= (-10) • 2 : (-5)
= (-20) : (-5)
= 4
(-10) • (-1) : ((2 - 7) : (5 - 3)) = 10 : ((-5) : 2)
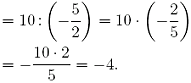
Definition Der Abstand einer rationalen Zahl x von der Zahl Null heißt Betrag von x, geschrieben IxI.
Es gilt: |0| = 0 , |1| = 1 , |-1| = 1 |  Merke Merke
Für alle x, y, z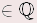 gilt das so genannte Distributivgesetz: gilt das so genannte Distributivgesetz:
x • (y + z) = x • y + x • z
x • (y - z) = x • y - x • z |
Konkret heißt das -
Ein Bruch der Form 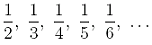 heißt Stammbruch. heißt Stammbruch. -
Brüche der Form 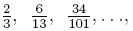 bei denen der Zähler kleiner als der Nenner ist, heißen echte Brüche. bei denen der Zähler kleiner als der Nenner ist, heißen echte Brüche. -
Umgekehrt heißen Brüche der Form 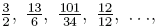 bei denen der Zähler größer oder gleich dem Nenner ist, unechte Brüche. bei denen der Zähler größer oder gleich dem Nenner ist, unechte Brüche. -
Brüche der Form 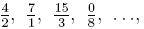 bei denen der Zähler ein Vielfaches des Nenners ist, heißen Scheinbrüche. bei denen der Zähler ein Vielfaches des Nenners ist, heißen Scheinbrüche. Anmerkung
Ein unechter Bruch, der kein Scheinbruch ist, lässt sich als so genannte gemischte Zahl darstellen. Beispiel 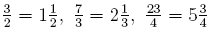
|  Merke Merke
Die gemischte Zahl 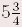 darf nicht mit dem Produkt darf nicht mit dem Produkt 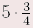 verwechselt werden. verwechselt werden. |
Konkret heißt das: Die Umformung 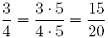 heißt Erweitern des Bruches heißt Erweitern des Bruches 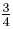 mit 5. mit 5.
Entsprechend heißt die Umformung 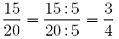 Kürzen des Bruches Kürzen des Bruches 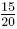 mit 5. mit 5.
Beim Erweitern und beim kürzen bleibt der Wert des Bruches gleich, lediglich die Form des Bruches ändert sich. |  Merke Merke
Für alle a, c 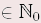 und alle b, d und alle b, d 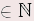 gilt: gilt: 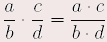 | Beispiel 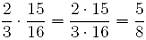
|  Merke Merke
Für alle a 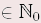 und alle b, c, d und alle b, c, d 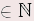 gilt: gilt: 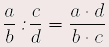
| Beispiel 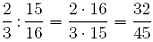
|  Merke Merke
Brüche mit dem Nenner 10 oder 100 oder 1000 oder 10000... lassen sich als so genannte Dezimalzahlen schreiben. Es gilt: 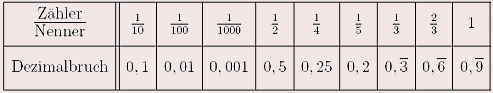
Anmerkung:
Mit Dezimalzahlen wird auf jeden Fall dann richtig gerechnet, wenn sie in "normale" Brüche umgewandelt werden. |
Beispiel
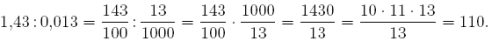 |