|
Unterrichtseinheit
Mechanik und Akustik
|
Akustik - Die Lehre vom Schall | Schallerreger | Schallüberträger | Schallempfänger | | Gitarre
Radio
Sänger
Motor... | Luft
Wasser
... |  Ohr
Mikrophon
... |
Die Erregung des Schalls
|  Versuch Versuch
Schallerreger Beobachte die Schwingungen die Schallerreger verursachen. | Beobachtung | - Fühle den Kehlkopf beim Sprechen.
- Beobachte eine Gitarrensaite.
- Beobachte eine Stimmgabel.
- Beobachte eine Lautsprechermembran.
| | Ergebnis | Schallerreger machen schnelle Schwingbewegungen. | | |  Versuch Versuch
Faden- und Federpendel Bei dem Versuch beobachtet man die Schwingbewegungen von Faden- und Federpendel. | Beobachtung | | Fadenpendel | Federpendel | 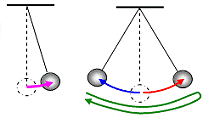 | 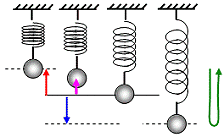 | positive Amplitude a (= maximaler Abstand vom Nullniveau)
negative Amplitude a
Eine Periode mit Periodendauer T
s = Momentaner Abstand
| Wir beobachten langsame Schwingbewegungen. | | Ergebnis | - Die Schwingbewegung ist eine periodische hin- und hergehende Bewegung.
- Feder- und Fadenpendel führen gedämpfte Schwingungen durch.
- Eine Schwingung wird durch die Periodendauer T und die Amplitude a gekennzeichnet.
| | |  Versuch Versuch
Messung der Periodendauer (=Schwingungsdauer) Bei diesem Versuch kann man feststellen, wie man am besten die Periodendauer errechnet. | Beobachtung | 1. Messart: Wir messen 5 Einzelschwingungen und berechnen den Mittelwert:
Faden = 1 m; a = 10 cm; m = 100 g; T1 = 1,1 s
T2 = 1,0 s
T3 = 1,0 s
T4 = 0,9 s
T5 = 1,0 s
Mittelwert:
T = (T1 + T2 + T3 + T4 + T5) : 5 = 1,0 s 2. Messart: Wir messen die Zeit t für n (z.B. n = 10) Schwingungen und berechnen daraus die Zeit T für eine Einzelschwingung. | | Ergebnis | Einzelne Schwingungsdauer  bzw. T = bzw. T = 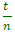 | | | Aufgabe / Lösung  | Gegegeben: n = 20; t = 30 s.
Gesucht: T | |  | Wegen T = t/n gilt: T = 30s/20 = 1,5 s | | | | Aufgabe / Lösung  | Was bedeutet:
T = 0,2 s
T = 0,002 s
T = 2 s | |  | T = 0,2 s : In 1 s werden 5 Perioden durchlaufen.
T = 0,002 s : In 1 s werden 500 Perioden durchlaufen.
T = 2 s : In 1 s werden 0,5 Perioden durchlaufen. | | | |  Merke Merke
Die Zahl der Schwingungen je Sekunde nennt man Frequenz f. |
Beispiel Ein Körper führt 1000 Perioden in 2,5 s aus:
Dann gilt für die Frequenz f = n/t = 1000/2,5 s = 400/1 s = 400 • 1/s = 400 Hz
Periodendauer und Frequenz beim Fadenpendel
Beispiele Betrachte die Schwingungsbewegung am Besten so, dass die Zeit gerade startet
(t = 0s), wenn das Pendel ganz links in der maximalen Auslenkung ist. Pendel 1  | Dies ist ein sehr langsam schwingendes Pendel:
Von der maximalen Auslenkung links bis zur Mitte benötigt es etwa 1 s, bis zur maximalen Auslenkung rechts vergeht eine weitere Sekunde.
Nach 3 s ist es wieder in der Mitte und nach 4 s erreicht es den Ausgangspunkt links. | | Danach beginnt der Pendelvorgang erneut, eine Periode ist zu Ende. Die Zeit für eine Periode nennt man die Periodendauer T.
Die Periodendauer ist bei diesem Pendel T = 4 s. Die Zahl der Schwingungen in einer Sekunde bezeichnet man als Frequenz f.
In einer Sekunde schafft dieses Pendel 1/4 seiner Pendelbewegung, seine Frequenz ist also f = 1/4 Hz. | Pendel 2 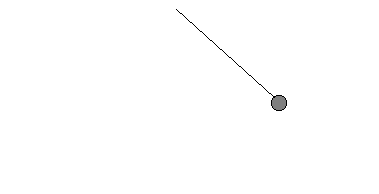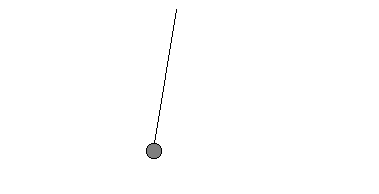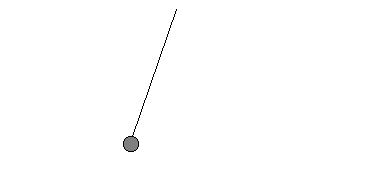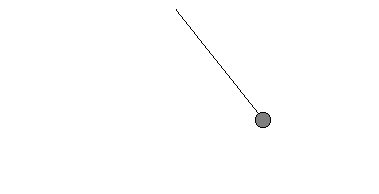 | Es schwingt schneller.
Diesmal dauert es von ganz links nach ganz rechts nur 1 s,
zurück wieder nur 1 s.
Die Periodendauer ist hier
T = 2 s.
In einer Sekunde schafft das Pendel die Hälfte (1/2) seiner Pendelbewegung, seine Frequenz ist damit f = 1/2 Hz. | Pendel 3 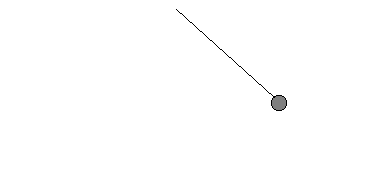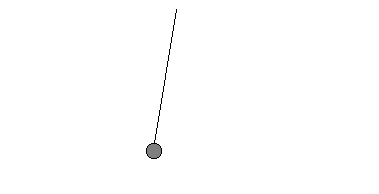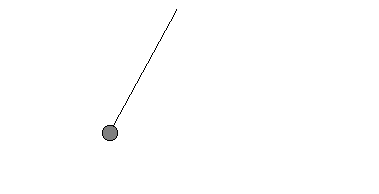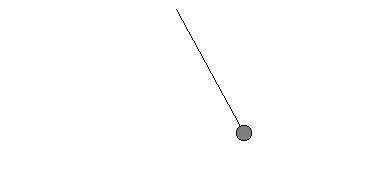 | Dieses Pendel ist ein "Sekundenpendel".
Die Periodendauer ist hier
T = 1 s.
In jeder Sekunde schafft das Pendel genau eine Pendelbewegung, die Frequenz ist damit f = 1 Hz. | Pendel 4 Benötigt das Pendel für eine Schwingung nur eine halbe Sekunde —› T = 1/2 s,
dann schafft es in einer Sekunde zwei Schwingungen —› f = 2 Hz. Pendel 5 Ein Pendel, das für eine Schwingung nur T = 1/4s benötigt,
macht in einer Sekunde 4 Schwingungen, hat also die Frequenz f = 4Hz. Zusammenstellung dieser Ergebnisse | Pendel | Periodendauer T | Frequenz f | | 1 | 4 s | 1/4 Hz | | 2 | 2 s | 1/2 Hz | | 3 | 1 s | 1 Hz | | 4 | 1/2 s | 2 Hz | | 5 | 1/4 s | 4 Hz |
Aufzeichnung
| Aufgabe / Lösung  | Wie kann man Schwingungen aufzeichnen? | |  | .gif)
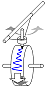
1. Schreibstimmgabel
Schwingung deutlich sichtbar.
Sehr kleine Amplitude.
|  | 
2. Bleistiftpendel
Gedämpfte Schwingungen.
Amplituden nehmen ab. |
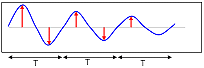
 | 3. Oszilloskop-Aufzeichnung Ungedämpfte Schwingungen.
Amplituden bleiben konstant. 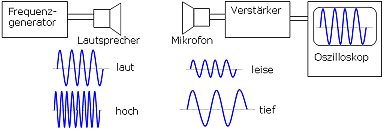
|
 | 4. Magnetaufzeichnung (z.B.: Tonbandkassette) |
 | 5. Digitale Aufzeichnung (z.B.: CD, DVD, Festplatte) | | |
Ausbreitung des Schalls
Wie breitet sich Schall aus?
Wie gelangt er von der Schallquelle zum Ohr? |  Versuch Versuch
Klingel in Vakuumglocke Bei dem Versuch befindet sich eine Klingel unter einer Vakuumglocke.
Man testet dabei, ob man die Klingel weiterhin hört.
| Beobachtung | 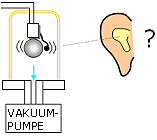 | | Ergebnis | Im leeren Raum (Vakuum) kann sich kein Schall ausbreiten. | | |  Versuch Versuch
Metallstab zwischen mechan. Uhr und Ohr Bei diesem Versuch wird zwischen der mechanischen Uhr und dem Ohr ein Metallstab angebracht.
| Beobachtung | 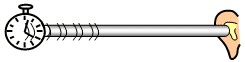
| | Ergebnis | Der Metallstab dient als Schallleitung.
Zur Schallleitung sind Gase, feste Körper und Flüssigkeiten geeignet. Bsp.:
Schwimmbad: Hören unter Wasser.
Hören an Eisenbahnschienen. | | |  Versuch Versuch
Magnetrollenbahn Was kann man bei einer Magnetrollenbahn beobachten? | Beobachtung | 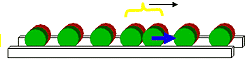
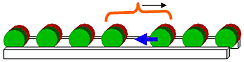 | | Ergebnis | Als Folge eines Stoßes wandert im Schallleiter eine Verdichtung nach rechts. Die Einzelteilchen bewegen sich dabei nur um kurze Strecken nach rechts. Verdünnungen wandern ebenfalls nach rechts.
Die Einzelteile wandern dabei nach links. | | |  Merke Merke
Schall breitet sich dadurch aus, dass aufeinander folgende Verdichtungen und Verdünnungen durch den Schallleiter wandern. | |  Merke Merke
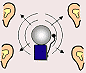
Schall breitet sich in Luft allseitig aus. |
Schallgeschwindigkeit
| Aufgabe / Lösung  | Wie schnell breitet sich Schall aus?
Beispiel:
Ein Blitz schlägt in Baum (Abstand s ≈ 1,5 km) ein, nach Zeit t = 5 s hört man den Donner. Berechne die Schallgeschwindigkeit v. | |  | Die Geschwindigkeit gibt eine zurückgelegte Strecke pro Zeiteinheit an.
Also: Man teilt die Strecke s durch die Zeit t und erhält die Strecke, die der Schall pro Sekunde zurücklegt.
Formel: v = s/t Rechnung:
v ≈ 1,5 km / 5 s ≈ 1500 m / 5 s ≈ 300 m/s | | | |  Versuch Versuch
Genauere Methode mit Digitaluhr Beobachte die Schwingungen die Schallerreger verursachen. | Beobachtung | 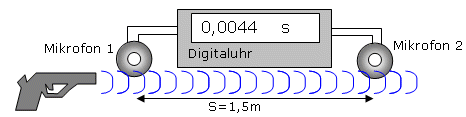
| | Ergebnis | Rechnung: v = s/t = 1,5 m / 0,0044 s ≈ 340 m/s Die Schallgeschwindigkeit beträgt - in Luft 340 m/s
- in Wasser 1480 m/s
- in Eisen 5800 m/s
| | | Aufgabe / Lösung  | Ein Echo kehrt nach 3 Sekunden zurrück. Wie weit ist die Echowand entfernt? | |  | Gegeben: t = 3s; v = 340m/s
Gesucht: s
Es gilt: v = s/t
Umgeformt: s = v • t Zahlen werden eingesetzt: s = 340 m/s • 3 s = 1020 m
1020 m / 2 = 510m
Antwort: Die Echowand ist 510 m entfernt. | | | Das Echo  Von Echo spricht man, wenn der reflektierte Schall erheblich später beim Hörer eintrifft als der direkte Schall: der Zeitunterschied Von Echo spricht man, wenn der reflektierte Schall erheblich später beim Hörer eintrifft als der direkte Schall: der Zeitunterschied 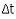 beträgt mehrere Sekunden. beträgt mehrere Sekunden.
Nachhall Trifft der reflektierte Schall beim Hörer schon ein, bevor die Silbe oder das Wort ganz ausgesprochen ist, nennt man dies Nachhall. Schallbeugung Der Schall breitet sich in der Luft nicht nur geradlinig aus. Richtungshöre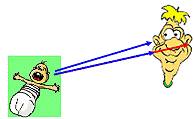 n n Wenn die beiden Ohren den Schall einer sich seitlich befindlichen Schallquelle nach
unterschiedlichen Laufzeiten empfangen, kann das Gehirn aus dem Laufzeitunterschied die Richtung der Schallquelle feststellen. |